PART 2: Understanding historical energy revolutions will help us in our quest to halt global warming. There are two important questions to ask history about and apply to our current challenge:
How large, meaning what is the scale, of a potential energy revolution, and how long will it take? To answer these questions, we’ll examine the English Industrial Revolution (EIR), which has been, so far, the greatest energy revolution in history.
Let’s examine energy prices during the EIR.
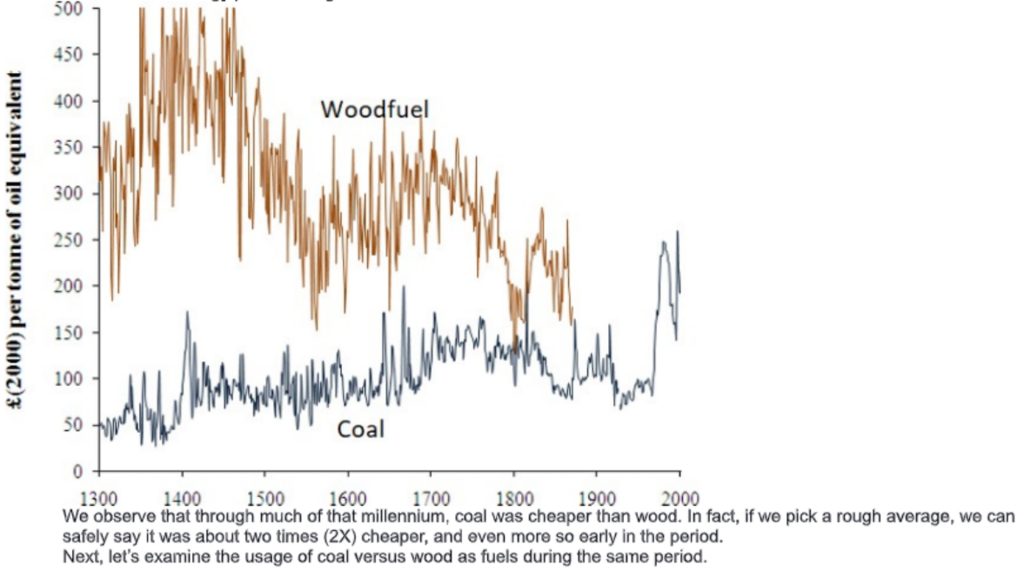
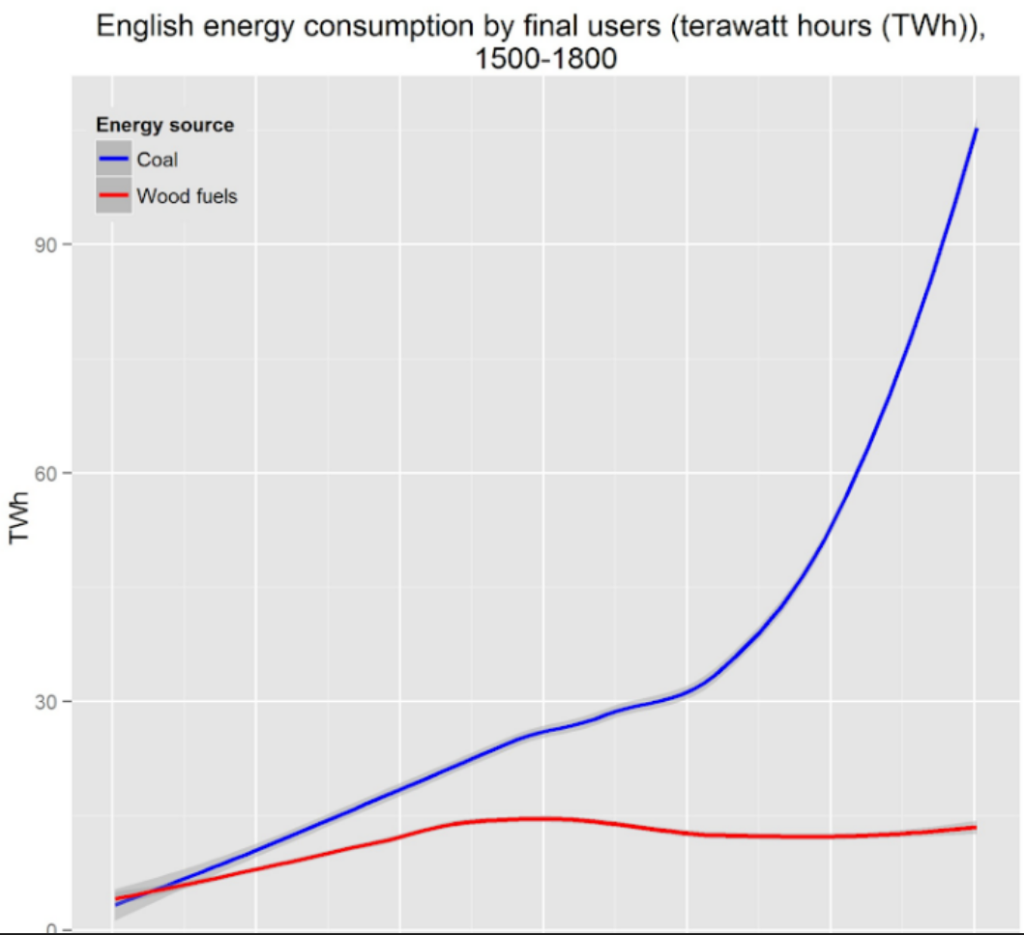
Clearly starting in about 1500, coal usage exceeded wood usage, and the difference in favor of coal continued to widen. The simplest explanation for this is that coal was much cheaper. There is an implementation lag due to needing new infrastructure for the new fuel. This graph gives us an idea of how large the replacement scale was, and can be. Now let’s examine the duration of the EIR. For this, we can use data about the output of the economy, something economists label as Gross Domestic Product or GDP.
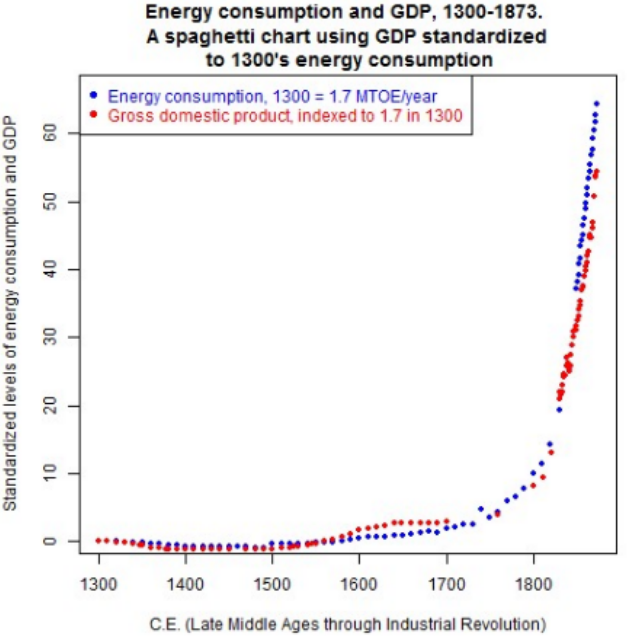
This graph shows the great acceleration, in constant prices, of GDP after 1500 and continuing thereafter. For our purposes, I will pick a period of 150 years, from 1600 through 1750, that constituted the bulk of the transition to modern economic growth and that just continues accelerating thereafter, including through today. But that 150-year period is crucial because of the large infrastructure changes that were necessary. Notice also the very close connection between energy inputs and economic outputs.
Next, we can apply the history lessons to our major energy challenges. To do this, we will use some very basic economics that helps us think about the substitution of one commodity for another based on price differences. The fancy name is cross-price substitution or substitution elasticity. Algebra is the easy way to think about this, so to the blackboard.

This elasticity formula uses an elasticity “index” of one (1) that is from research provided by the Energy Information Agency. The one is plugged into the elasticity formula. Next let’s say we can find an energy source that is 20 times cheaper than anything we have now. That is plugged into the denominator as a -2000% price change. All that is left is to calculate the numerator, which yields a -2000% (20 times) reduction in carbon source usage by substituting it with the new cheap source. The conclusion is that if we can find such a source, carbon energy source use will be essentially completely replaced. Fortunately, science suggests we do have such sources. The example I am using here uses an estimated cost reduction
using the new science of Condensed Matter Nuclear Physics (CMNS). A group of scientists from around the world are actively working to make such energy scalable and commercial. One of this group, Jed Rothwell, provides engineering estimates that suggest CMNS energy sources should start at 20 times cheaper and then become much cheaper over time, for example, an order-of-magnitude cheaper.
